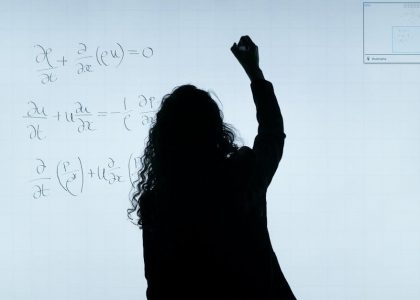Spacetime, a four-dimensional continuum, unites space and time, while number theory explores mathematical structures like primes. Their intersection reveals deep computational and structural connections, reshaping our understanding of reality.
1.1. Overview of Spacetime in Physics
Spacetime, a four-dimensional continuum, unites space and time, fundamental to physics, especially relativity. Introduced by Einstein, it describes the universe as a dynamic fabric where mass and energy warp its geometry. Spacetime diagrams visualize events and particle paths, aiding in understanding relativistic effects like time dilation. The Lorentz transformation shows how space and time measurements mix across reference frames. This framework is essential for phenomena like motion and gravity, illustrating spacetime’s active role beyond a passive backdrop. Its structure and dynamics are central to modern physics, shaping our comprehension of cosmic interactions and the universe’s evolution. Spacetime’s study remains pivotal in theoretical advancements.
1.2. Basics of Number Theory
Number theory is a branch of mathematics focusing on the properties and relationships of integers. It examines prime numbers, their distribution, and factors, as well as solutions to equations involving integers, such as Diophantine equations. The field also explores algebraic structures like rings and fields. Prime numbers, fundamental to cryptography, are a central topic. Diophantine equations seek integer solutions, linking number theory to geometry. Additionally, algebraic number theory extends these concepts to complex numbers. These principles are foundational in mathematics and have applications in computer science and cryptography, while also offering insights into the computational nature of spacetime in theoretical physics.
1.3. The Intersection of Spacetime and Number Theory
The intersection of spacetime and number theory proposes a computational vision of spacetime, where time emerges from discrete mathematical operations. This perspective, influenced by theories like quantum gravity and digital physics, suggests that spacetime is made of fundamental computational units. Number theory, particularly prime numbers and hypergraphs, plays a crucial role in modeling this structure. The passage of time is seen as a sequence of computational updates, mirroring the progression of a hypergraph. This vision bridges physics and mathematics, offering new insights into the nature of reality, where spacetime is not just a passive backdrop but an active, computational entity.

Historical Background
The concept of spacetime evolved from classical physics, while number theory traces its roots to ancient mathematics. Both fields saw transformative advancements in the 19th and 20th centuries;

2.1. Development of Spacetime in Physics
The concept of spacetime emerged from classical physics, evolving through Newtonian mechanics and Maxwell’s equations. By the late 19th century, physicists like Einstein revolutionized the understanding of space and time, introducing relativity. Einstein’s theory of spacetime as a four-dimensional continuum transformed physics, showing that time and space are relative and interconnected. The Lorentz transformation mathematically described spacetime’s structure, enabling modern physics to unify space and time into a single entity. This development laid the foundation for quantum mechanics and cosmology, reshaping humanity’s understanding of the universe.
2.2. Evolution of Number Theory in Mathematics
Number theory, the study of integers and their properties, traces its roots to ancient civilizations, including Babylonian, Egyptian, and Greek mathematicians. The Pythagoreans explored number properties, while Diophantus pioneered algebraic methods with Diophantine equations. The Islamic Golden Age and Indian scholars advanced decimal systems and algebraic techniques. Fermat’s Last Theorem in the Renaissance period spurred centuries of inquiry. The 19th and 20th centuries saw formalization into algebraic and analytic number theory, with Gauss’s contributions shaping modern study. Today, number theory thrives in cryptography and prime number research, driving ongoing mathematical exploration and innovation.
2.3. Key Figures in the Study of Spacetime and Number Theory
Albert Einstein revolutionized spacetime with his theory of relativity, introducing the four-dimensional continuum. Hermann Minkowski provided the mathematical framework, while David Hilbert contributed to its formalization. In number theory, Carl Friedrich Gauss laid the foundation with his works on primes and modular arithmetic. Srinivasa Ramanujan made groundbreaking discoveries in partition functions and prime number distribution. These figures bridged the gap between spacetime and number theory, inspiring modern visions where spacetime is viewed as a computational entity, with hypergraphs modeling its structure and computation underpinning time itself.
Key Concepts in Spacetime
Spacetime is a four-dimensional continuum fusing space and time, with relativity governing its mechanics. Time emerges computationally, reflecting irreversible processes, while hypergraphs model its structure dynamically.
3.1. The Four-Dimensional Continuum
The four-dimensional continuum of spacetime integrates three spatial dimensions with one time dimension, forming a unified fabric. This structure, central to relativity, describes events as points in spacetime, with coordinates (x, y, z, t). The continuum is flat in special relativity but curved by mass and energy in general relativity. Visualizations, like spacetime diagrams, depict world-lines of particles and light paths, illustrating motion and causality. The interplay of space and time in this framework reveals the dynamic and relational nature of physical reality, where geometry and gravity are inherently linked.
3.2. Relativity and Lorentz Transformations
Relativity, rooted in Einstein’s theories, describes how spacetime’s geometry and physical laws remain consistent across inertial frames. The Lorentz transformation mathematically relates space and time coordinates between observers in relative motion. It introduces time dilation, length contraction, and relativity of simultaneity, challenging classical notions of absolute space and time. The transformation preserves the spacetime interval, ensuring consistency of physical phenomena. In the number-theoretic vision, these transformations align with computational processes, suggesting spacetime’s structure is fundamentally tied to computation. This interplay underscores the deep connection between relativity, geometry, and number theory, offering a new lens to interpret spacetime’s nature.
3.3. Visualization of Spacetime Through Diagrams

Spacetime diagrams, such as Minkowski diagrams, visually represent the four-dimensional continuum, aiding in understanding relativistic effects. These diagrams depict world-lines of particles, showing their paths through space and time. Light paths appear as diagonal lines, illustrating the speed of light as a universal limit. Such visualizations help explain time dilation, length contraction, and the relativity of simultaneity. By plotting events and their causal relationships, diagrams reveal the structure of spacetime, making abstract concepts like spacetime intervals and Lorentz transformations more intuitive. These tools are essential for grasping the interplay of space and time in both classical relativity and number-theoretic interpretations of spacetime.

Key Concepts in Number Theory
Prime numbers, Diophantine equations, and algebraic structures form the core of number theory, exploring integer solutions, distributions, and abstract algebraic systems that underpin mathematical reasoning.
4.1. Prime Numbers and Their Distribution
Prime numbers, fundamental to number theory, are integers greater than 1 with no positive divisors other than 1 and themselves. Their distribution among natural numbers is irregular yet intriguing, with gaps between primes varying unpredictably. The Prime Number Theorem describes their density, showing primes become less frequent as numbers grow larger. Despite their seemingly random distribution, primes exhibit patterns, such as twin primes and arithmetic progressions. Understanding their distribution deepens insights into number theory’s foundational questions and has implications for cryptography and computational mathematics.

4.2. Diophantine Equations and Their Solutions
Diophantine equations are polynomial equations seeking integer solutions, playing a central role in number theory. Examples include ax² + by² = c, such as the Pythagorean theorem. These equations often arise in problems involving divisibility and modular arithmetic. Solving them requires advanced techniques like Fermat’s infinite descent or elliptic curve theory. The study of Diophantine equations reveals deep insights into number distributions and structures, with applications in cryptography and computational mathematics. Despite their complexity, these equations have led to breakthroughs in understanding prime numbers and algebraic structures, making them a cornerstone of modern number theory research.
4.3. Algebraic Number Theory
Algebraic number theory extends classical number theory by studying algebraic structures, particularly in number fields, which are finite extensions of the rational numbers. Key concepts include field extensions, rings of integers, and ideals, which provide a framework for analyzing properties like divisibility and factorization in more complex settings. Tools such as Galois theory and class field theory are central to understanding these structures. The study of zeta functions and L-functions further reveals deep connections between algebraic objects and analytic properties. This field has profound implications for cryptography, coding theory, and the resolution of Diophantine equations, making it a cornerstone of modern mathematics.

The Number Theoretic Vision of Spacetime
Spacetime is reimagined as a computational framework, where hypergraphs model interactions, and time emerges from irreducible computations, blending geometry with number theory in a unified vision of reality.
5.1. Spacetime as a Computational Entity
Spacetime is envisioned as a computational entity where time’s passage reflects computational processes. Hypergraphs model interactions, with time emerging from irreducible computations. This framework suggests spacetime’s structure and evolution are inherently tied to computation, challenging traditional geometric views and offering novel insights into its nature.
5.2. The Role of Hypergraphs in Modeling Spacetime
Hypergraphs emerge as powerful tools for modeling spacetime, capturing complex relationships between spatial and temporal entities. Unlike traditional graphs, hypergraphs can connect multiple nodes, representing intricate spacetime interactions. This approach allows for the integration of spatial dimensions and time, enabling a unified framework. Hypergraphs also facilitate the representation of world-lines, depicting particles’ paths through spacetime. Their flexibility makes them ideal for encoding relativistic effects and Lorentz transformations. By abstracting spacetime as a hypergraph, researchers can explore its structural properties and dynamic evolution, offering new insights into the interplay of space, time, and matter.
5.3. The Relationship Between Time and Computation
Time is fundamentally computational, with its passage reflecting the execution of computations. In the number-theoretic vision of spacetime, the progression of time corresponds to the incremental updating of the hypergraph, making time necessary for maintaining spatial structure. This perspective treats spacetime as a dynamic, computational entity where events unfold through irreducible steps. The relationship between time and computation underscores the intrinsic link between the fabric of spacetime and the processes that govern it, suggesting that time itself is a manifestation of computational activity.

Implications of the Number Theoretic Vision
The number-theoretic vision of spacetime integrates time and computation, offering new perspectives on reality. It suggests that spacetime emerges from computational processes, blending geometry with arithmetic.
6.1. Philosophical Implications
The number-theoretic vision of spacetime challenges traditional views by suggesting that time and space are computational entities. This perspective blurs the line between abstract mathematics and physical reality, implying that spacetime emerges from number-theoretic structures. The idea that time is fundamentally computational raises profound questions about free will and determinism. If time reflects computational processes, does it preclude genuine randomness, or is reality inherently algorithmic? Additionally, the vision suggests a universe where mathematical truths are not just descriptors but foundational to existence, echoing Platonism. This framework invites philosophers to rethink causality, reality, and the nature of existence itself.
6.2. Technological Applications
The number-theoretic vision of spacetime opens novel avenues for technological innovation. Hypergraphs, as models of spacetime, could revolutionize quantum computing by enabling more efficient algorithms. Computational spacetime aligns with quantum mechanics, potentially advancing quantum error correction. Additionally, this framework could enhance data processing by treating spacetime as a computational fabric, optimizing tasks like network optimization and AI. The vision also suggests new approaches to simulation technology, enabling precise modeling of complex systems. Finally, it could inspire breakthroughs in cryptography, leveraging number-theoretic properties for secure communication; These applications highlight the transformative potential of merging spacetime physics with number theory.
6.3. Future Research Directions
Future research should explore the computational foundations of spacetime, linking number theory to quantum mechanics. Developing hypergraph models for spacetime could unlock new quantum algorithms. Investigating the interplay between prime number distributions and spacetime geometry may reveal hidden patterns. Additionally, studying how spacetime’s structure influences computational complexity could deepen our understanding of reality. Experimental verification of these concepts, such as testing computational irreducibility in physical systems, is essential. Interdisciplinary collaboration between physicists and number theorists will drive innovation, potentially leading to breakthroughs in quantum computing, cryptography, and our fundamental understanding of the universe’s mathematical fabric.
The integration of spacetime and number theory offers profound insights into the computational nature of reality, bridging physics and mathematics. This vision reshapes our understanding of time and space, revealing their deep interconnections and fostering interdisciplinary exploration.
7.1. Summary of Key Points
The integration of spacetime and number theory reveals a profound computational structure underlying reality. Spacetime, as a four-dimensional continuum, is intertwined with number theory’s principles, offering insights into the fabric of the universe. Key concepts include spacetime as a computational entity, the role of hypergraphs in modeling, and the relationship between time and computation. These ideas challenge traditional views of physics and mathematics, suggesting a unified, number-theoretic vision of spacetime. The implications span philosophical, technological, and interdisciplinary collaborations, paving the way for future research and innovation in understanding the cosmos.
7.2. Potential for Interdisciplinary Collaboration
The fusion of spacetime and number theory fosters unprecedented collaboration between physicists, mathematicians, and computer scientists. Physicists gain new tools to model spacetime computationally, while mathematicians find novel applications for number theory. Computer scientists contribute algorithms to simulate these structures, enabling breakthroughs in quantum computing and cosmology. This interdisciplinary approach not only enriches each field but also accelerates technological advancements, such as more efficient algorithms and deeper insights into the universe’s fundamental nature. By bridging these disciplines, the number-theoretic vision of spacetime opens new avenues for innovation and understanding, promising transformative discoveries in the years to come.
7.3. Final Thoughts on the Vision
The number-theoretic vision of spacetime offers a profound shift in understanding the cosmos, blending physics and mathematics. By viewing spacetime as a computational entity, it posits that time’s passage reflects computation, linking space and time inseparably. This framework hints at a unified theory, where number theory’s structures underpin reality. The vision challenges traditional views, suggesting that spacetime’s fabric is inherently mathematical. While philosophical questions arise, the potential for technological and theoretical breakthroughs is immense. This vision inspires future research, urging scientists to explore its depths and implications, promising transformative discoveries in physics, mathematics, and beyond.